Fourier dönüşümü: özellikleri, uygulamaları, örnekleri ve alıştırmalar
Fourier dönüşümü, bütünleşik dönüşüm ailesine ait bütünleştirilebilir işlevlere yönelik bir analitik uyarlama yöntemidir. F (t) fonksiyonlarının Cos (t) ve Sen (t) cinsinden yeniden tanımlanmasından oluşur.
Bu fonksiyonların trigonometrik kimlikleri, türetme ve antiderivasyon özellikleri ile birlikte, Fourier dönüşümünü aşağıdaki karmaşık fonksiyon aracılığıyla tanımlamaya hizmet eder:

Bu, ifade anlamlı olduğu sürece, yani uygunsuz integral yakınsak olduğunda geçerlidir. Cebirsel olarak Fourier dönüşümünün doğrusal bir homeomorfizm olduğu söylenir.
Fourier dönüşümü ile çalışılabilecek her fonksiyon tanımlanmış bir parametrenin dışında boş olmalıdır.
özellikleri

Fourier dönüşümü aşağıdaki özelliklere uygundur:
varoluş
Fourier dönüşümünün, gerçekler R'de tanımlanan f (t) fonksiyonunda varlığını doğrulamak için aşağıdaki 2 aksiyomun yerine getirilmesi gerekir:
- f (t) tüm R için parçalara süreklidir
- f (t) R'ye entegre edilebilir
Fourier dönüşümünün doğrusallığı
M (t) ve N (t), tanımlanmış Fourier dönüşümleri ile herhangi bir a ve b sabitleriyle herhangi iki işlev olsun.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)
Aynı zamanda aynı adı taşıyan integralin doğrusallığına da dayanıyor.
Bir türevin Fourier dönüşümü
Tüm gerçeklerde sürekli ve bütünleştirilebilir bir fonksiyona sahibiz, burada:

Ve f (f ')' nin türevi süreklidir ve R boyunca parçalar halinde tanımlanmıştır.
Bir türevin Fourier dönüşümü, aşağıdaki ifadelerle bölümlerle bütünleşerek tanımlanır:
F [f '(t)] (z) = iz F [f (t)] (z)
Yüksek mertebeden türevlerde, tüm n1 için yapmanız gerekenler, homolog bir şekilde uygulanacaktır:
F [fn '(t)] (z) = (iz) n F [f (t)] (z)
Fourier dönüşümünün farklılaşması
Tüm gerçeklerde sürekli ve bütünleştirilebilir bir fonksiyona sahibiz, burada:
i (d / dz) F [f (t)] (z) = F [t. f (t)] (z)
Bir çevirinin Fourier dönüşümü
Her şeye θ küme S ve T’ye ait olan S her şeye göre,
F [ τ a θ] = e-iay F [ θ] F [ τ a T ] = e-iax F [ T]
Τ ile vektör üzerinde çeviri operatörü olarak çalışan bir a.
Fourier dönüşümünün çevirisi
Her şeye θ küme S ve T’ye ait olan S her şeye göre,
τ a F [θ] = F [e-iax . F ] τ a F [T ] = F [e-ıay . T]
R'ye ait olanların hepsi için
Ölçek grubunun Fourier dönüşümü
Her şey için θ S grubuna ait S. T grubuna ait.
λ - {0} 'e ait olmanız gerekenler:
F [θ (λx)] = (1 / | λ |) F [θ] ( y / λ )
F [T (λx)] = (1 / | λ |) F [T] (y / λ )
F sürekli ve açıkça bütünleşebilen bir işlevse, a> 0 olur. Sonra:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
Bu sonucu göstermek için değişken değişimine devam edebilirsiniz.
T → + sonra s = → + ∞ değerinde
T → - sonra s = → - ∞



simetri
Fourier dönüşümünün simetrisini incelemek için, Parseval kimliği ve Plancherel formülü doğrulanmalıdır.
S'ye ait θ ve δ'lar var . Oradan çıkarılabilir:

elde edilen
1 / (2π) d { F [θ ], F [δ ] } Parseval kimliği
1 / (2π) d / 2 || F [θ ] || L2Rd Plancherel formülü
Evrişimde bir ürünün Fourier dönüşümü
Laplace dönüşümünde benzer işlevlerin izlenmesiyle, fonksiyonların katılımı, Fourier dönüşümleri arasındaki ürünü ifade eder.
2 sınırlı, tanımlanmış ve tamamen entegre fonksiyonlar olarak f ve g'ye sahibiz:
F (f * g) = F (f). F (g)


Sonra değişkeni değiştirirken
t + s = x; uygunsuz çift katlı integralle devam ediyor



F (f) F (g) = F (f, G)
Süreklilik ve sonsuzluğa düşme
R'ye ait her şey için ,, F [ θ] Rd. 'Da sınırlanan sürekli fonksiyon kriterlerine uymaktadır.
Ayrıca { F [ θ] (y)} → 0 C ise | y | → ∞
tarih
Bu matematiksel kavram 1811'de Joseph B. Fourier tarafından sunulmuş ve bu esnada ısının yayılması üzerine bir inceleme geliştirildi . Çeşitli bilim ve mühendislik dalları tarafından hızla kabul edildi.
Laplace dönüşümü ile adi diferansiyel denklemler arasındaki çalışma ilişkisiyle karşılaştırıldığında bile, kısmi diferansiyel denklemlerin çalışılmasında ana çalışma aracı olarak kurulmuştur .
Fourier dönüşümü ne için kullanılır?
Temel olarak, türetilmiş ifadeleri, bütünleştirilebilir polinomlar biçimindeki diferansiyel ifadeleri ifade eden güç elemanlarına dönüştürürken, denklemleri büyük ölçüde basitleştirmeye hizmet eder.
Optimizasyonda, sonuçların modülasyonu ve modellenmesi standartlaştırılmış bir ifade olarak hareket eder, birkaç kuşaktan sonra mühendislik için sıkça kullanılan bir kaynaktır.
Fourier serileri
Bunlar kosinüs ve meme cinsinden tanımlanır; Genel periyodik fonksiyonlarla çalışmayı kolaylaştırmaya hizmet ederler. Uygulandığında, kısmi ve adi diferansiyel denklemleri çözme tekniklerinin bir parçasıdır.
Fourier serisi, Taylor serisinden daha genel çünkü Taylor serisinde temsili olmayan periyodik sürekli olmayan fonksiyonlar geliştiriyorlar.
Fourier serisinin diğer formları
Fourier dönüşümünü analitik olarak anlamak için, Fourier serisini karmaşık gösteriminde tanımlayana kadar Fourier serisinin bulunabileceği diğer biçimleri gözden geçirmek önemlidir.
- 2L periyodlu bir fonksiyonda Fourier serisi
Bir Fourier serisinin yapısını, [-L, L] aralığında periyotu p = 2L> 0 olan periyodik fonksiyonlara uyarlamak gerekir.
- Tek ve hatta fonksiyonlarda Fourier serisi
Fonksiyonların simetrik özelliklerinden faydalanırken avantajlar sunan [-π, π] aralığı göz önünde bulundurulur.
F eşitse, Fourier serisi bir Cosines serisi olarak kurulur.

F tuhafsa, Fourier serisi bir Sinüs serisi olarak kurulur.

Fourier serisinin tamamlanmış notasyonu
Fourier serisinin gelişimi için tüm gereksinimleri karşılayan bir f (t) fonksiyonumuz varsa, karmaşık gösterimini kullanarak [-t, t] aralığında belirtmek mümkündür:

uygulamaları

Temel çözümün hesaplanması
Fourier dönüşümü, lineer tipte kısmi diferansiyel denklemlerin sabit katsayılı çalışmalarında güçlü bir araçtır. Sınırlandırılmamış alanlara sahip işlevler için eşit olarak başvururlar.
Laplace dönüşümü gibi, Fourier dönüşümü kısmi bir türev işlevi, kullanımı çok daha basit olan sıradan bir diferansiyel denkleme dönüştürür.
Isı denklemi için Cauchy problemi, çekirdek ısı fonksiyonunun veya Dirichlet çekirdeğinin üretildiği Fourier dönüşümünün sıkça uygulanacağı bir alan sunar .
Temel çözümün hesaplanmasına ilişkin olarak, Fourier dönüşümünü bulmanın yaygın olduğu yerlerde aşağıdaki durumlar sunulmuştur:
-Lablace Dizisi
-Sıcaklığın eklenmesi
-Schrödinger'in Özü
- Dalgaların dizilmesi
Sinyal teorisi
Fourier dönüşümünün bu dalda uygulanmasının genel nedeni, esas olarak bir sinyalin daha kolay işlenebilir sinyallerin sonsuz bir üst üste binmesi olarak karakteristik ayrışmasından kaynaklanmaktadır.
Bir ses dalgası veya elektromanyetik bir dalga olabilir, Fourier dönüşümü onu basit dalgaların üst üste binmesiyle ifade eder. Elektrik mühendisliğinde bu temsil oldukça sık görülür.
Öte yandan, Fourier dönüşümünün sinyal teorisi alanındaki uygulama örnekleri vardır:
-Sistemin tanımlanmasındaki problemler. Kurulan fyg
Çıkış sinyalinin tutarlılığı ile -Problem
Sinyalin filtrelenmesi ile ilgili sorunlar
Örnekler
Örnek 1
Aşağıdaki ifade için Fourier dönüşümünü tanımlayın:

Ayrıca şu şekilde de temsil edebiliriz:
F (t) = Sen (t) [H (t + k) - H (t - k) ]
Dikdörtgen darbe tanımlanmıştır:
p (t) = H (t + k) - H (t - k)
Fourier dönüşümü, modülasyon teoremine benzeyen aşağıdaki ifadeye uygulanır.
f (t) = p (t) Sen (t)
Nerede: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
Ve Fourier dönüşümü şu şekilde tanımlanır:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Örnek 2
İfade için Fourier dönüşümünü tanımlayın:


F (h) eşit bir fonksiyon olduğu için söylenebilir


Parçalar ile entegrasyon değişkenler ve farklılıkları aşağıdaki gibi seçilerek uygulanır
u = günah (zh) du = z cos (zh) dh
dv = s (eh) 2 v = (eh) 2/2
Sahip olduğunuzu değiştirme

Temel hesaplama teoremi altında değerlendirdikten sonra

Birinci mertebeden diferansiyel denklemlere ilişkin önceki bilgileri uygularken, ifade şu şekilde ifade edilir:

K elde etmek için değerlendiririz

Son olarak, ifadenin Fourier dönüşümü olarak tanımlanır.

Önerilen egzersizler
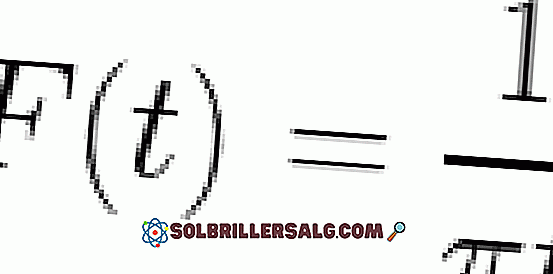

- W / (1 + w2) ifadesinin dönüşümünü al